Pendiente y ángulo de inclinación de una ladera. Estimación con el mapa

Podemos estimar la pendiente de una ladera fácilmente si estamos situados en el mapa con suficiente precisión. Para ello basta medir la distancia horizontal, $\Delta\,\ell$, entre dos puntos $A$ y $B$ que estén sobre la ladera (teniendo en cuenta la escala del mapa) y entre los cuales las curvas de nivel estén separadas uniformemente, procurando que los puntos elegidos den un segmento $s=[A,B]$ lo más perpendicular posible a todas y cada una de las curvas de nivel comprendidas entre dischos punto.

Contando ahora el número curvas de nivel que median entre los dos puntos y teniendo en cuenta la equistancia entre ellas &medash;suele ser de 20 m entre dos curvas consecutivas en los mapas cartográficos a escala $1:25\,000$, obtendremos la diferencia de altitud, $\Delta\,h$ entre la curva que passa por el punto $A$ y la que passa por el punto $B$. Entonces, la pendiente de la ladera (del plano inclinado) es (por definición) el cociente $\dfrac{\Delta\,h}{\Delta\,\ell}$, que es el valor de la tangente trigonométrica del ángulo $\alpha$ que forma el plano inclinado con el plano horizontal (dibujemos mentalmente el triángulo rectángulo). Así, por ejemplo, si encontramos que la distancia (a «vuelo de pájaro») entre $A$ y $B$ es de $\Delta\,\ell=200\,\text{m}$ y un desnivel entre $A$ y $B$, el valor de la pendiente de dicha ladera es de $\dfrac{150}{200}=0.75=75\,\%$; es decir $\tan\,\alpha=0.75$.

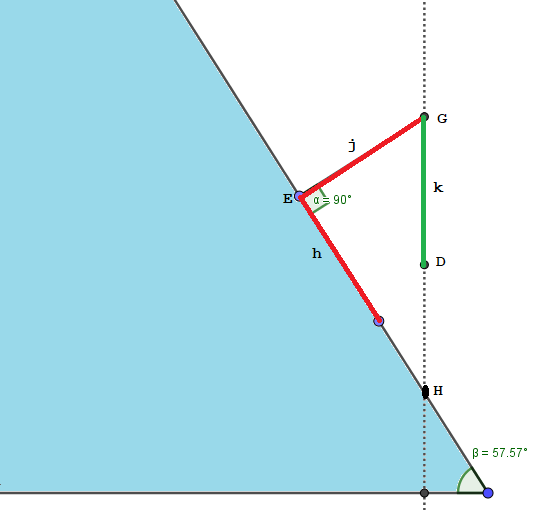
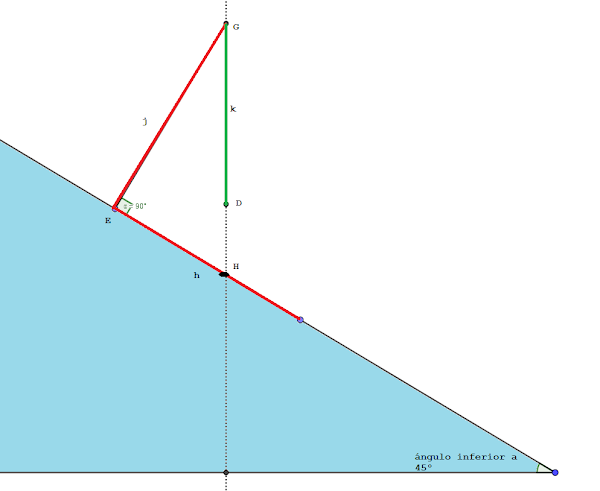
Para conocer el valor del ángulo $\alpha$ —dato importante para gestionar lo mejor posible el riesgo por el peligro de aludes, a la hora de tomar decisiones— basta tener en cuenta, grosso modo, que un plano inclinado con a un ángulo de $45^{\circ}$ le corresponde una pendiente $\tan\,45^{\circ}=1$, esto es, una pendiente del $100\,\%$; así que para valores de la pendiente estimada inferiores a $1$, el ángulo será inferior a $45^{\circ}$, y para valores superiores a $1$ el ángulo correspondiente es superior a $45^{\circ}$. Si se quiere conocer el valor de dicho ángulo con precisión, podemos ayudarnos de la capacidad de cálculo trigonométrico elemental que tenemos con la calculadora científica que tengamos instalada en nuestro smart phone. Así, para el valor de la pendiente del ejemplo, $\tan{\alpha}=0.75$, el ángulo de inclinación que le corresponde es (recíproca de la tangente) $\alpha=\text{tan}^{-1}(0.75)\approx 37^{\circ}$. $\diamond$

Técnicas de orientación: situación por intersección de dos arcos capaces

Es bien sabido que para situarnos en el mapa podemos triangular la posición con dos puntos de referència identificables en el terreno y trazar las rectas con con las demoras respectivas que habremos medido con la brújula —a veces se hace con tres, formando un triángulo cuyo incentro nos da con más precisión nuestra situación—. Sin embargo, también podemos hacerlo mediante la intersección de dos arcos capaces.

Recordemos que el arco capaz de un segmento de recta $s=[A,B]$] —los puntos extremos son $A$ y $B$—, de amplitud angular dada $\alpha$, se define como el lugar geométrico desde el que se observa dicho segmento bajo dicha amplitud angular; este lugar geométrico es un arco de circunferencia.

Escribí un artículo en mi blog de náutica acerca de esta técnica que os invito a leer. $\diamond$

Estimación de pendientes que corresponden a ángulos de inclinación inferiores o superiores a $45^{\circ}$ con ayuda de los bastones de senderismo/esquí

En el artículo anterior exponía un método de medida estimativa del ángulo de inclinación de laderas próximo a $30^{\circ}$ empleando los bastones de esquí/senderismo. En éste voy a presentar una variante del mismo que es útil para estimar el ángulo de inclinación (con respecto al plano horizontal) de laderas con una inclinación próxima a $45^{\circ}$. Estimar el ángulo de inclinación nos puede venir bien en actividades en las que tengamos que superar, previsiblemente, laderas o corredores con este grado de inclinación. Veremos, primero, la situación geométrica que nos encontraremos al disponer los bastones tal como se muestra en las figura 1, cuando el ángulo de inclinación de la ladera es de $45^{\circ}$ (figura 1); y, como en el artículo anterior, analizaremos de qué manera se alejan de esta situación los casos de mayor o menor inclinación. Para ello, me voy a ayudar de las figuras 2 y 3, que corresponden respectivamente a cada una de dichas situaciones. Tengamos en cuenta que es importante conocer aproximadamente la inclinación de la pendiente de las laderas en las actividades en la alta montaña invernal para poder gestionar correctamente el riesgo que podemos asumir en cuando a la información de que dispondremos de los boletines de peligro de aludes así como de las condiciones nivológicas observadas, ya que en el caso de encontrarnos con un peligro elevado (incluso moderado), desde luego, habrá que evitar preceptivamente las pendientes de gran exposición superiores a dicho valor del ángulo de inclinación, e incluso los superiores a $30^{\circ}$, tomando decisiones conservadoras, incluso la de abortar la actividad programada.

Inclinación (de referéncia) correspondiente a un ángulo $45^{\circ}$
Esta situación la tomaremos como punto de partida en la exposición que sigue. Veamos primero qué tipo de triángulo se configura sobre el terreno inclinado al servirnos convenientemente del par de bastones de esquí (o senderismo). En las figuras uno de los bastones los pintaré en rojo —llamaré a éste «el primer& bastón» y lo designaré con las letras $h$ o $k$—, y en verde al «segundo bastón» que designaré también con la letras $j$.

Regulados ambos bastones a la misma altura —el que sean telecópicos facilitará las cosas—, se trata de poner el primero sobre el terreno inclinado, encarado sobre la línea de máxima pendiente; y haremos unas marcas sobre el suelo en cada uno de sus extremos —es mejor que el mango del bastón mire ahora hacia abajo (la punta hacia arriba) para facilitar el levantarlo girando sobre dicha punta clavada en el suelo y trasladar la longitud del mismo sobre la recta perpendicular al plano inclinado —¡ojo!, no al plano horizontal como hacíamos para hacer estimaciones alrededor de los treinta grados de inclinación—. Iremos levantando este primer bastón girándolo pues hacia arriba: pivotando sobre la punta del mismo (clavada en el suelo) hasta colocarlo en posición perpendicular al plano inclinado (véase la figura 1: segmento $j$). Hecho esto, suspenderemos el segundo baston del extremo del primero (segmento $k$), a modo de plomada, de manera que, como podremos comprobar, la vertical del extremo (punto $D$ en la figura) que pende quedará sobre la marca, $H$, que hemos hecho sobre el plano inclinado con el primer bastón. Como el ángulo que forma la ladera con el plano horizontal ha de ser igual al ángulo complementario de $\angle DHE$ y, al formarse un triángulo rectángulo isósceles, $\measuredangle DHE = 45^{\circ}$, entonces la inclinación de la ladera es igual a $90^{\circ}-45^{\circ}=45^{\circ}$.

Figura 1

Ángulos de inclinación superiores a $45^{\circ}$
En el caso de que la pendiente del terreno inclinado sea mayor que la que le corresponde a un ángulo de $45^{\circ}$, cláramente tendremos una situación como la que ilustro a continuación en la figura 2; en tal caso, al suspender el segundo baston del extremo del primero (segmento $k$), la vertical del extremo (punto $D$ en la figura) que pende quedará más abajo de la marca $H$.

Figura 2

Ángulos de inclinación inferiores a $45^{\circ}$
Si la pendiente del terreno inclinado es menor que la que le corresponde a un ángulo de $45^{\circ}$, la situación que se plantea la ilustro en la figura 3. Ahora, al suspender el segundo baston del extremo del primero (segmento $k$), la vertical del extremo (punto $D$ en la figura) que pende quedará más arriba de la marca $H$.

Figura 3

$\square$
-oOo-
Observaciones:
Desde luego, huelga comentar que el uso de un inclinómetro nos daría más rapidez y precisión. Algunas brújulas lo llevan incorporado, si bien suelen ser algo más pesadas y menos versátiles que las brújulas más utilizadas en alpinismo (las cartográficas, de base transparente), que no lo llevan.

Brújula cartográfica

Brújula con inclinómetro y nivel de horizontalidad, acoplada a un pequeño trípode, que ofrece también una muy buena precisión en la medida de ángulos horizontales

-oOo-
Aludes:
[1] AEMET: Boletín del peligro de aludes

Estimación de pendientes que corresponden a ángulos de inclinación inferiores o superiores a $30^{\circ}$ con ayuda de los bastones de senderismo/esquí

Para estimar la medida el ángulo que forma un terreno inclinado con el plano horizontal utilizando los bastones de esquí o senderismo, podemos centrarnos en la situación que voy a exponer a continuación, que es la de un terreno inclinado que forma un ángulo de $30^{\circ}$ con el plano horizontal, y ver como se alejan de ésta los casos en que la pendiente es mayor y menor respectivamente que la que presenta en dicho caso de referencia. Para ello, me voy a ayudar de tres figuras que corresponden a cada una de dichas situaciones. Tengamos en cuenta que es importante conocer aproximadamente la inclinación de la pendiente de las laderas en las actividades en la alta montaña invernal para poder gestionar correctamente el riesgo que podemos asumir en cuando a la información de que dispondremos de los boletines de peligro de aludes, ya que en el caso de encontrarnos con un peligro elevado —recordemos la escala europea de previsión del peligro de aludes consta de cinco grados, numerados del $1$ (débil) al $5$ (muy fuerte)— habrá que evitar preceptivamente las pendientes superiores a $30^\circ$ a partir del grado $3$ de la escala de peligro de aludes en las previsiones, tomando decisiones conservadoras (primando la seguridad), y, si es necesario, abortando la actividad.

Inclinación (de referéncia) correspondiente a un ángulo $30^{\circ}$
Esta situación la tomaremos como punto de partida en la exposición que sigue. Veamos primero qué tipo de triángulo se configura sobre el terreno inclinado al servirnos convenientemente del par de bastones de esquí (o senderismo). Nos proponemos comprobar que el ángulo de inclinación de la ladera es $30^\circ$ a partir de la configuración geométrica que se forma disponiendo los bastones como se indica a continuación. En las figuras uno de los bastones lo pintaré en rojo —llamaré a éste «el primer& bastón» y lo designaré con las letras $h$ o $k$—, y en verde al «segundo bastón» que designaré también con la letras $j$.

Regulados ambos bastones a la misma altura —el que sean telecópicos facilitará las cosas—, se trata de poner el primero sobre el terreno inclinado, encarado sobre la línea de máxima pendiente; y haremos unas marcas sobre el suelo en cada uno de sus extremos —es mejor que el mango del bastón mire hacia arriba para facilitar el levantarlo girando sobre la punta clavada en el suelo y trasladar la longitud del mismo sobre la recta perpendicular al plano horizontal, tal como a continuación voy a explicar—.

Ahora, levantaremos este primer bastón girándolo hacia arriba tal como hemos indicado: pivotando sobre la punta del mismo (clavada en el suelo) hasta colocarlo en posición perpendicular a la base del plano inclinado (véase la figura 1: segmento $j$). Pues bien, si el tercer lado, $k$, medido con el otro bastón tiene la misma longitud que los otros dos, el triángulo que se configura sobre el terreno inclinado es necesáriamente equilátero, y, por tanto, cada uno de sus tres ángulos medirá $60^\circ$. En consecuencia, el ángulo que forma el terreno inclinado con la base del mismo tendrá que ser el complementario del ángulo $\measuredangle\,GDE$ (ángulo del vértice inferior derecho del triángulo), luego la medida del ángulo que forma la ladera con el plano horizontal ha de ser $\measuredangle\,DBH=90^{\circ}-60^{\circ}=30^{\circ}$.

Figura 1

Ángulos de inclinación superiores a $30^{\circ}$
En el caso de que la pendiente del terreno inclinado (de la ladera) sea mayor que la que le corresponde a un ángulo de $30^{\circ}$, cláramente tendremos una situación como la que ilustro a continuación en la figura 2; en tal caso, con el segundo bastón ya no será posible conformar el triángulo equilátero del que hablábamos en la situación de referencia, y el extremo derecho del mismo estará a la derecha del punto $G$ (extremo superior del primer bastón).

Figura 2

Ángulos de inclinación inferiores a $30^{\circ}$
Por otra parte, si el ángulo que forma el terreno inclinado con el plano horizontal fuese menor de $30^{\circ}$ nos encontraríamos con una situación como la de la figura 3; el triángulo equilátero de la primera situación tampoco puede formarse: en este caso, el extremo derecho del segundo bastón, $k$, se sitúa a la izquierda del extremo $G$ del primer bastón, $j$, colocado en posición perpendicular al plano horizontal.

Figura 3

$\square$
-oOo-
Aludes:
[1] AEMET: Boletín del peligro de aludes
[2] AEMET: Escala Europea de Peligro de Aludes: http://www.aemet.es/es/conocermas/montana/detalles/escala_peligro_aludes

Ajustant els crampons automàtics a les noves botes rígides

Bota rígida per a activitats invernals d'alta muntanya (model Fitz Roy, de la marca mallorquina Bestard)

Estimación del grado de inclinación de una pendiente con los bastones de esquí/senderismo

Para estimar la medida el ángulo que forma un terreno inclinado con el plano horizontal utilizando los bastones de esquí o senderismo, podemos centrarnos en la situación que voy a exponer a continuación, que es la de un terreno inclinado que forma un ángulo de $30^{\circ}$ con el plano horizontal, y ver como se alejan de ésta los casos en que la pendiente es mayor y menor respectivamente que la que presenta en dicho caso de referencia. Para ello, me voy a ayudar de tres figuras que corresponden a cada una de dichas situaciones. Tengamos en cuenta que es importante conocer aproximadamente la inclinación de la pendiente de las laderas en las actividades en la alta montaña invernal para poder gestionar correctamente el riesgo que podemos asumir en cuando a la información de que dispondremos de los boletines de peligro de aludes, ya que en el caso de encontrarnos con un peligro elevado habrá que evitar preceptivamente las pendientes superiores a $\measuredangle\,DBH=30^\circ$.

Inclinación (de referéncia) correspondiente a un ángulo $30^{\circ}$
Esta situación la tomaremos como punto de partida en la exposición que sigue. Veamos primero qué tipo de triángulo se configura sobre el terreno inclinado al servirnos convenientemente del par de bastones de esquí (o senderismo). Nos proponemos comprobar que ángulo $\measuredangle\,DBH=30^\circ$. En las figuras uno de los bastones lo pintaré en rojo —llamaré a éste «el primer& bastón» y lo designaré con las letras $h$ o $k$—, y en verde al «segundo bastón» que designaré también con la letras $j$.

Regulados ambos bastones a la misma altura —el que sean telecópicos facilitará las cosas—, se trata de poner el primero sobre el terreno inclinado, encarado sobre la línea de máxima pendiente; y haremos unas marcas sobre el suelo en cada uno de sus extremos —es mejor que el mango del bastón mire hacia arriba para facilitar el levantarlo girando sobre la punta clavada en el suelo y trasladar la longitud del mismo sobre la recta perpendicular al plano horizontal, tal como a continuación voy a explicar—.

Ahora, levantaremos este primer bastón girándolo hacia arriba tal como hemos indicado: pivotando sobre la punta del mismo (clavada en el suelo) hasta colocarlo en posición perpendicular a la base del plano inclinado (véase la figura 1: segmento $j$). Pues bien, si el tercer lado, $k$, medido con el otro bastón tiene la misma longitud que los otros dos, el triángulo que se configura sobre el terreno inclinado es necesáriamente equilátero, y, por tanto, cada uno de sus tres ángulos medirá $60^\circ$. En consecuencia, el ángulo que forma el terreno inclinado con la base del mismo tendrá que ser el complementario del ángulo $\measuredangle\,GDE$, luego su medida será $\measuredangle\,DBH=30^\circ$

Figura 1

Ángulos de inclinación superiores a $30^{\circ}$
En el caso de que la pendiente del terreno inclinado sea mayor que la que le corresponde a un ángulo de $30^{\circ}$, cláramente tendremos una situación como la que ilustro a continuación en la figura 2; en tal caso, con el segundo bastón ya no será posible conformar el triángulo equilátero del que hablábamos arriba, y el extremo derecho del mismo estará a la derecha del punto $G$ (extremo superior del primer bastón).

Figura 2

Ángulos de inclinación inferiores a $30^{\circ}$
Por otra parte, si el ángulo que forma el terreno inclinado con el plano horizontal fuese menor de $30^{\circ}$ nos encontraríamos con una situación como la de la figura 3; el triángulo equilátero de la primera situación tampoco puede formarse: en este caso, el extremo derecho del segundo bastón, $k$, se sitúa a la izquierda del extremo $G$ del primer bastón, $j$, colocado en posición perpendicular al plano horizontal.

Figura 3

$\square$
-oOo-
Referencias:
[1] AEMET: Boletín del peligro de aludes