Estimación de pendientes que corresponden a ángulos de inclinación inferiores o superiores a $45^{\circ}$ con ayuda de los bastones de senderismo/esquí

En el artículo anterior exponía un método de medida estimativa del ángulo de inclinación de laderas próximo a $30^{\circ}$ empleando los bastones de esquí/senderismo. En éste voy a presentar una variante del mismo que es útil para estimar el ángulo de inclinación (con respecto al plano horizontal) de laderas con una inclinación próxima a $45^{\circ}$. Estimar el ángulo de inclinación nos puede venir bien en actividades en las que tengamos que superar, previsiblemente, laderas o corredores con este grado de inclinación. Veremos, primero, la situación geométrica que nos encontraremos al disponer los bastones tal como se muestra en las figura 1, cuando el ángulo de inclinación de la ladera es de $45^{\circ}$ (figura 1); y, como en el artículo anterior, analizaremos de qué manera se alejan de esta situación los casos de mayor o menor inclinación. Para ello, me voy a ayudar de las figuras 2 y 3, que corresponden respectivamente a cada una de dichas situaciones. Tengamos en cuenta que es importante conocer aproximadamente la inclinación de la pendiente de las laderas en las actividades en la alta montaña invernal para poder gestionar correctamente el riesgo que podemos asumir en cuando a la información de que dispondremos de los boletines de peligro de aludes así como de las condiciones nivológicas observadas, ya que en el caso de encontrarnos con un peligro elevado (incluso moderado), desde luego, habrá que evitar preceptivamente las pendientes de gran exposición superiores a dicho valor del ángulo de inclinación, e incluso los superiores a $30^{\circ}$, tomando decisiones conservadoras, incluso la de abortar la actividad programada.

Inclinación (de referéncia) correspondiente a un ángulo $45^{\circ}$
Esta situación la tomaremos como punto de partida en la exposición que sigue. Veamos primero qué tipo de triángulo se configura sobre el terreno inclinado al servirnos convenientemente del par de bastones de esquí (o senderismo). En las figuras uno de los bastones los pintaré en rojo —llamaré a éste «el primer& bastón» y lo designaré con las letras $h$ o $k$—, y en verde al «segundo bastón» que designaré también con la letras $j$.

Regulados ambos bastones a la misma altura —el que sean telecópicos facilitará las cosas—, se trata de poner el primero sobre el terreno inclinado, encarado sobre la línea de máxima pendiente; y haremos unas marcas sobre el suelo en cada uno de sus extremos —es mejor que el mango del bastón mire ahora hacia abajo (la punta hacia arriba) para facilitar el levantarlo girando sobre dicha punta clavada en el suelo y trasladar la longitud del mismo sobre la recta perpendicular al plano inclinado —¡ojo!, no al plano horizontal como hacíamos para hacer estimaciones alrededor de los treinta grados de inclinación—. Iremos levantando este primer bastón girándolo pues hacia arriba: pivotando sobre la punta del mismo (clavada en el suelo) hasta colocarlo en posición perpendicular al plano inclinado (véase la figura 1: segmento $j$). Hecho esto, suspenderemos el segundo baston del extremo del primero (segmento $k$), a modo de plomada, de manera que, como podremos comprobar, la vertical del extremo (punto $D$ en la figura) que pende quedará sobre la marca, $H$, que hemos hecho sobre el plano inclinado con el primer bastón. Como el ángulo que forma la ladera con el plano horizontal ha de ser igual al ángulo complementario de $\angle DHE$ y, al formarse un triángulo rectángulo isósceles, $\measuredangle DHE = 45^{\circ}$, entonces la inclinación de la ladera es igual a $90^{\circ}-45^{\circ}=45^{\circ}$.

Figura 1

Ángulos de inclinación superiores a $45^{\circ}$
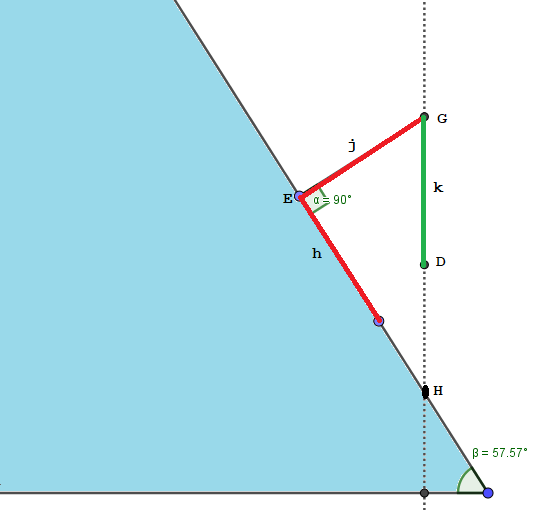
En el caso de que la pendiente del terreno inclinado sea mayor que la que le corresponde a un ángulo de $45^{\circ}$, cláramente tendremos una situación como la que ilustro a continuación en la figura 2; en tal caso, al suspender el segundo baston del extremo del primero (segmento $k$), la vertical del extremo (punto $D$ en la figura) que pende quedará más abajo de la marca $H$.

Figura 2

Ángulos de inclinación inferiores a $45^{\circ}$
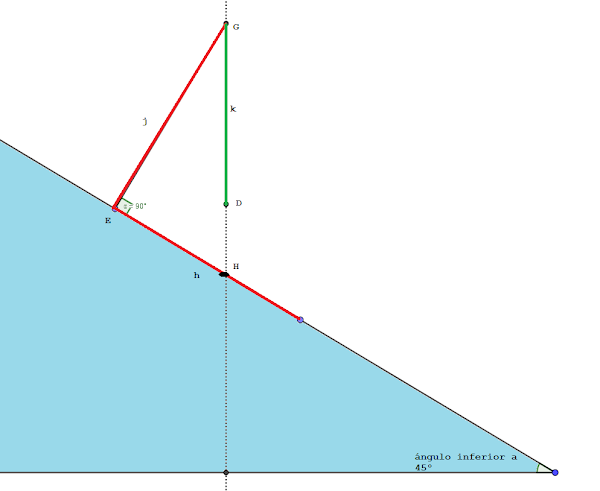
Si la pendiente del terreno inclinado es menor que la que le corresponde a un ángulo de $45^{\circ}$, la situación que se plantea la ilustro en la figura 3. Ahora, al suspender el segundo baston del extremo del primero (segmento $k$), la vertical del extremo (punto $D$ en la figura) que pende quedará más arriba de la marca $H$.

Figura 3

$\square$
-oOo-
Observaciones:
Desde luego, huelga comentar que el uso de un inclinómetro nos daría más rapidez y precisión. Algunas brújulas lo llevan incorporado, si bien suelen ser algo más pesadas y menos versátiles que las brújulas más utilizadas en alpinismo (las cartográficas, de base transparente), que no lo llevan.

Brújula cartográfica

Brújula con inclinómetro y nivel de horizontalidad, acoplada a un pequeño trípode, que ofrece también una muy buena precisión en la medida de ángulos horizontales

-oOo-
Aludes:
[1] AEMET: Boletín del peligro de aludes